Comparison of six regridding algorithms
xESMF exposes five different regridding algorithms from the ESMF library:
bilinear:ESMF.RegridMethod.BILINEARconservative:ESMF.RegridMethod.CONSERVEconservative_normed:ESMF.RegridMethod.CONSERVEpatch:ESMF.RegridMethod.PATCHnearest_s2d:ESMF.RegridMethod.NEAREST_STODnearest_d2s:ESMF.RegridMethod.NEAREST_DTOS
where conservative_normed is just the conservative method with the normalization set to ESMF.NormType.FRACAREA instead of the default norm_type=ESMF.NormType.DSTAREA.
This notebook demonstrates how these algorithms behave in different situations.
Notes
bilinearandconservativeshould be the most commonly used methods. They are both monotonic (i.e. will not create new maximum/minimum).Nearest neighbour methods, either source to destination (s2d) or destination to source (d2s), could be useful in special cases. Keep in mind that d2s is highly non-monotonic.
Patch is ESMF’s unique method, producing highly smooth results but quite slow.
From the ESMF documentation:
The weight \(w_{ij}\) for a particular source cell \(i\) and destination cell \(j\) are calculated as \(w_{ij}=f_{ij} * A_{si}/A_{dj}\). In this equation \(f_{ij}\) is the fraction of the source cell \(i\) contributing to destination cell \(j\), and \(A_{si}\) and \(A_{dj}\) are the areas of the source and destination cells.
For
conservative_normed,… then the weights are further divided by the destination fraction. In other words, in that case \(w_{ij}=f_{ij} * A_{si}/(A_{dj}*D_j)\) where \(D_j\) is fraction of the destination cell that intersects the unmasked source grid.
Detailed explanations are available on ESMPy documentation.
Preparation
[1]:
%matplotlib inline
import matplotlib.pyplot as plt
import cartopy.crs as ccrs
import numpy as np
import xarray as xr
import xesmf as xe
method_list = [
"bilinear",
"conservative",
"conservative_normed",
"nearest_s2d",
"nearest_d2s",
"patch",
]
[2]:
ds_in = xe.util.grid_global(20, 15) # input grid
ds_fine = xe.util.grid_global(4, 4) # high-resolution target grid
ds_coarse = xe.util.grid_global(30, 20) # low-resolution target grid
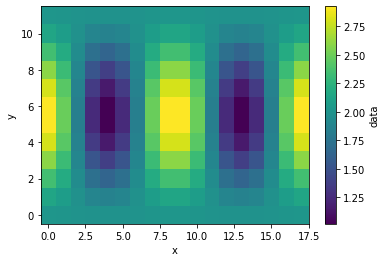
Make a wave field that is widely used in regridding benchmarks.
[3]:
ds_in["data"] = xe.data.wave_smooth(ds_in["lon"], ds_in["lat"])
ds_in
[3]:
<xarray.Dataset>
Dimensions: (y: 12, x: 18, y_b: 13, x_b: 19)
Coordinates:
lon (y, x) float64 -170.0 -150.0 -130.0 -110.0 ... 130.0 150.0 170.0
lat (y, x) float64 -82.5 -82.5 -82.5 -82.5 ... 82.5 82.5 82.5 82.5
lon_b (y_b, x_b) int64 -180 -160 -140 -120 -100 ... 100 120 140 160 180
lat_b (y_b, x_b) int64 -90 -90 -90 -90 -90 -90 -90 ... 90 90 90 90 90 90
Dimensions without coordinates: y, x, y_b, x_b
Data variables:
data (y, x) float64 2.016 2.009 1.997 1.987 ... 1.987 1.997 2.009 2.016- y: 12
- x: 18
- y_b: 13
- x_b: 19
- lon(y, x)float64-170.0 -150.0 ... 150.0 170.0
- standard_name :
- longitude
array([[-170., -150., -130., -110., -90., -70., -50., -30., -10., 10., 30., 50., 70., 90., 110., 130., 150., 170.], [-170., -150., -130., -110., -90., -70., -50., -30., -10., 10., 30., 50., 70., 90., 110., 130., 150., 170.], [-170., -150., -130., -110., -90., -70., -50., -30., -10., 10., 30., 50., 70., 90., 110., 130., 150., 170.], [-170., -150., -130., -110., -90., -70., -50., -30., -10., 10., 30., 50., 70., 90., 110., 130., 150., 170.], [-170., -150., -130., -110., -90., -70., -50., -30., -10., 10., 30., 50., 70., 90., 110., 130., 150., 170.], [-170., -150., -130., -110., -90., -70., -50., -30., -10., 10., 30., 50., 70., 90., 110., 130., 150., 170.], [-170., -150., -130., -110., -90., -70., -50., -30., -10., 10., 30., 50., 70., 90., 110., 130., 150., 170.], [-170., -150., -130., -110., -90., -70., -50., -30., -10., 10., 30., 50., 70., 90., 110., 130., 150., 170.], [-170., -150., -130., -110., -90., -70., -50., -30., -10., 10., 30., 50., 70., 90., 110., 130., 150., 170.], [-170., -150., -130., -110., -90., -70., -50., -30., -10., 10., 30., 50., 70., 90., 110., 130., 150., 170.], [-170., -150., -130., -110., -90., -70., -50., -30., -10., 10., 30., 50., 70., 90., 110., 130., 150., 170.], [-170., -150., -130., -110., -90., -70., -50., -30., -10., 10., 30., 50., 70., 90., 110., 130., 150., 170.]]) - lat(y, x)float64-82.5 -82.5 -82.5 ... 82.5 82.5
- standard_name :
- latitude
array([[-82.5, -82.5, -82.5, -82.5, -82.5, -82.5, -82.5, -82.5, -82.5, -82.5, -82.5, -82.5, -82.5, -82.5, -82.5, -82.5, -82.5, -82.5], [-67.5, -67.5, -67.5, -67.5, -67.5, -67.5, -67.5, -67.5, -67.5, -67.5, -67.5, -67.5, -67.5, -67.5, -67.5, -67.5, -67.5, -67.5], [-52.5, -52.5, -52.5, -52.5, -52.5, -52.5, -52.5, -52.5, -52.5, -52.5, -52.5, -52.5, -52.5, -52.5, -52.5, -52.5, -52.5, -52.5], [-37.5, -37.5, -37.5, -37.5, -37.5, -37.5, -37.5, -37.5, -37.5, -37.5, -37.5, -37.5, -37.5, -37.5, -37.5, -37.5, -37.5, -37.5], [-22.5, -22.5, -22.5, -22.5, -22.5, -22.5, -22.5, -22.5, -22.5, -22.5, -22.5, -22.5, -22.5, -22.5, -22.5, -22.5, -22.5, -22.5], [ -7.5, -7.5, -7.5, -7.5, -7.5, -7.5, -7.5, -7.5, -7.5, -7.5, -7.5, -7.5, -7.5, -7.5, -7.5, -7.5, -7.5, -7.5], [ 7.5, 7.5, 7.5, 7.5, 7.5, 7.5, 7.5, 7.5, 7.5, 7.5, 7.5, 7.5, 7.5, 7.5, 7.5, 7.5, 7.5, 7.5], [ 22.5, 22.5, 22.5, 22.5, 22.5, 22.5, 22.5, 22.5, 22.5, 22.5, 22.5, 22.5, 22.5, 22.5, 22.5, 22.5, 22.5, 22.5], [ 37.5, 37.5, 37.5, 37.5, 37.5, 37.5, 37.5, 37.5, 37.5, 37.5, 37.5, 37.5, 37.5, 37.5, 37.5, 37.5, 37.5, 37.5], [ 52.5, 52.5, 52.5, 52.5, 52.5, 52.5, 52.5, 52.5, 52.5, 52.5, 52.5, 52.5, 52.5, 52.5, 52.5, 52.5, 52.5, 52.5], [ 67.5, 67.5, 67.5, 67.5, 67.5, 67.5, 67.5, 67.5, 67.5, 67.5, 67.5, 67.5, 67.5, 67.5, 67.5, 67.5, 67.5, 67.5], [ 82.5, 82.5, 82.5, 82.5, 82.5, 82.5, 82.5, 82.5, 82.5, 82.5, 82.5, 82.5, 82.5, 82.5, 82.5, 82.5, 82.5, 82.5]]) - lon_b(y_b, x_b)int64-180 -160 -140 -120 ... 140 160 180
array([[-180, -160, -140, -120, -100, -80, -60, -40, -20, 0, 20, 40, 60, 80, 100, 120, 140, 160, 180], [-180, -160, -140, -120, -100, -80, -60, -40, -20, 0, 20, 40, 60, 80, 100, 120, 140, 160, 180], [-180, -160, -140, -120, -100, -80, -60, -40, -20, 0, 20, 40, 60, 80, 100, 120, 140, 160, 180], [-180, -160, -140, -120, -100, -80, -60, -40, -20, 0, 20, 40, 60, 80, 100, 120, 140, 160, 180], [-180, -160, -140, -120, -100, -80, -60, -40, -20, 0, 20, 40, 60, 80, 100, 120, 140, 160, 180], [-180, -160, -140, -120, -100, -80, -60, -40, -20, 0, 20, 40, 60, 80, 100, 120, 140, 160, 180], [-180, -160, -140, -120, -100, -80, -60, -40, -20, 0, 20, 40, 60, 80, 100, 120, 140, 160, 180], [-180, -160, -140, -120, -100, -80, -60, -40, -20, 0, 20, 40, 60, 80, 100, 120, 140, 160, 180], [-180, -160, -140, -120, -100, -80, -60, -40, -20, 0, 20, 40, 60, 80, 100, 120, 140, 160, 180], [-180, -160, -140, -120, -100, -80, -60, -40, -20, 0, 20, 40, 60, 80, 100, 120, 140, 160, 180], [-180, -160, -140, -120, -100, -80, -60, -40, -20, 0, 20, 40, 60, 80, 100, 120, 140, 160, 180], [-180, -160, -140, -120, -100, -80, -60, -40, -20, 0, 20, 40, 60, 80, 100, 120, 140, 160, 180], [-180, -160, -140, -120, -100, -80, -60, -40, -20, 0, 20, 40, 60, 80, 100, 120, 140, 160, 180]]) - lat_b(y_b, x_b)int64-90 -90 -90 -90 -90 ... 90 90 90 90
array([[-90, -90, -90, -90, -90, -90, -90, -90, -90, -90, -90, -90, -90, -90, -90, -90, -90, -90, -90], [-75, -75, -75, -75, -75, -75, -75, -75, -75, -75, -75, -75, -75, -75, -75, -75, -75, -75, -75], [-60, -60, -60, -60, -60, -60, -60, -60, -60, -60, -60, -60, -60, -60, -60, -60, -60, -60, -60], [-45, -45, -45, -45, -45, -45, -45, -45, -45, -45, -45, -45, -45, -45, -45, -45, -45, -45, -45], [-30, -30, -30, -30, -30, -30, -30, -30, -30, -30, -30, -30, -30, -30, -30, -30, -30, -30, -30], [-15, -15, -15, -15, -15, -15, -15, -15, -15, -15, -15, -15, -15, -15, -15, -15, -15, -15, -15], [ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [ 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15], [ 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30], [ 45, 45, 45, 45, 45, 45, 45, 45, 45, 45, 45, 45, 45, 45, 45, 45, 45, 45, 45], [ 60, 60, 60, 60, 60, 60, 60, 60, 60, 60, 60, 60, 60, 60, 60, 60, 60, 60, 60], [ 75, 75, 75, 75, 75, 75, 75, 75, 75, 75, 75, 75, 75, 75, 75, 75, 75, 75, 75], [ 90, 90, 90, 90, 90, 90, 90, 90, 90, 90, 90, 90, 90, 90, 90, 90, 90, 90, 90]])
- data(y, x)float642.016 2.009 1.997 ... 2.009 2.016
array([[2.01600962, 2.00851854, 1.99704154, 1.98694883, 1.98296291, 1.98694883, 1.99704154, 2.00851854, 2.01600962, 2.01600962, 2.00851854, 1.99704154, 1.98694883, 1.98296291, 1.98694883, 1.99704154, 2.00851854, 2.01600962], [2.1376148 , 2.0732233 , 1.97456981, 1.88781539, 1.85355339, 1.88781539, 1.97456981, 2.0732233 , 2.1376148 , 2.1376148 , 2.0732233 , 1.97456981, 1.88781539, 1.85355339, 1.88781539, 1.97456981, 2.0732233 , 2.1376148 ], [2.34824114, 2.18529524, 1.93564764, 1.71611122, 1.62940952, 1.71611122, 1.93564764, 2.18529524, 2.34824114, 2.34824114, 2.18529524, 1.93564764, 1.71611122, 1.62940952, 1.71611122, 1.93564764, 2.18529524, 2.34824114], [2.59145148, 2.31470476, 1.89070418, 1.51784433, 1.37059048, 1.51784433, 1.89070418, 2.31470476, 2.59145148, 2.59145148, 2.31470476, 1.89070418, 1.51784433, 1.37059048, 1.51784433, 1.89070418, 2.31470476, 2.59145148], [2.80207782, 2.4267767 , 1.85178201, 1.34614017, 1.14644661, 1.34614017, 1.85178201, 2.4267767 , 2.80207782, 2.80207782, 2.4267767 , 1.85178201, 1.34614017, 1.14644661, 1.34614017, 1.85178201, 2.4267767 , 2.80207782], ... [2.80207782, 2.4267767 , 1.85178201, 1.34614017, 1.14644661, 1.34614017, 1.85178201, 2.4267767 , 2.80207782, 2.80207782, 2.4267767 , 1.85178201, 1.34614017, 1.14644661, 1.34614017, 1.85178201, 2.4267767 , 2.80207782], [2.59145148, 2.31470476, 1.89070418, 1.51784433, 1.37059048, 1.51784433, 1.89070418, 2.31470476, 2.59145148, 2.59145148, 2.31470476, 1.89070418, 1.51784433, 1.37059048, 1.51784433, 1.89070418, 2.31470476, 2.59145148], [2.34824114, 2.18529524, 1.93564764, 1.71611122, 1.62940952, 1.71611122, 1.93564764, 2.18529524, 2.34824114, 2.34824114, 2.18529524, 1.93564764, 1.71611122, 1.62940952, 1.71611122, 1.93564764, 2.18529524, 2.34824114], [2.1376148 , 2.0732233 , 1.97456981, 1.88781539, 1.85355339, 1.88781539, 1.97456981, 2.0732233 , 2.1376148 , 2.1376148 , 2.0732233 , 1.97456981, 1.88781539, 1.85355339, 1.88781539, 1.97456981, 2.0732233 , 2.1376148 ], [2.01600962, 2.00851854, 1.99704154, 1.98694883, 1.98296291, 1.98694883, 1.99704154, 2.00851854, 2.01600962, 2.01600962, 2.00851854, 1.99704154, 1.98694883, 1.98296291, 1.98694883, 1.99704154, 2.00851854, 2.01600962]])
[4]:
ds_in["data"].plot()
[4]:
<matplotlib.collections.QuadMesh at 0x7fcc27f6db80>
[5]:
def regrid(ds_in, ds_out, dr_in, method):
"""Convenience function for one-time regridding"""
regridder = xe.Regridder(ds_in, ds_out, method, periodic=True)
dr_out = regridder(dr_in)
return dr_out
When dealing with global grids, we need to set periodic=True, otherwise data along the meridian line will be missing.
Increasing resolution
[6]:
for method in method_list:
print(method)
%time ds_fine[method] = regrid(ds_in, ds_fine, ds_in['data'], method)
print('')
bilinear
CPU times: user 386 ms, sys: 24.9 ms, total: 410 ms
Wall time: 408 ms
conservative
CPU times: user 66.8 ms, sys: 3.79 ms, total: 70.6 ms
Wall time: 70.4 ms
conservative_normed
CPU times: user 84.6 ms, sys: 266 µs, total: 84.9 ms
Wall time: 84.6 ms
nearest_s2d
CPU times: user 29.6 ms, sys: 0 ns, total: 29.6 ms
Wall time: 29.4 ms
nearest_d2s
CPU times: user 8.44 ms, sys: 0 ns, total: 8.44 ms
Wall time: 8.22 ms
patch
CPU times: user 420 ms, sys: 12.3 ms, total: 432 ms
Wall time: 431 ms
Nearest neighbour algorithms are very fast while the patch method is quite slow.
[7]:
fig, axes = plt.subplots(3, 2, figsize=[8, 8])
for i, method in enumerate(method_list):
ax = axes.flatten()[i]
ds_fine[method].plot.pcolormesh(ax=ax)
ax.set_title(method, fontsize=15)
plt.tight_layout()
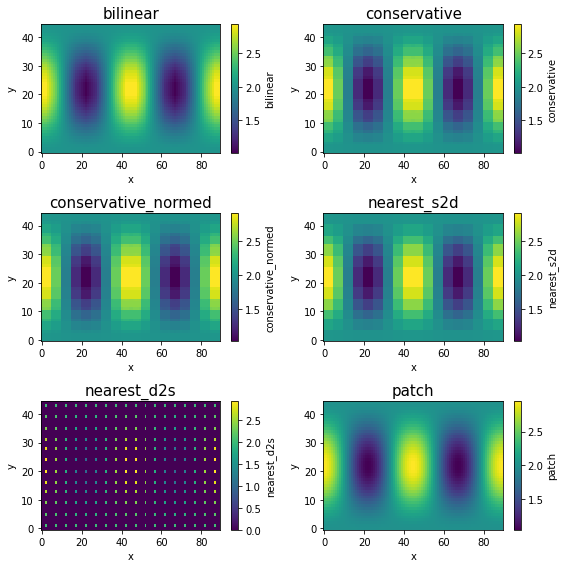
When regridding from low-resolution to high-resolution, bilinear and patch will produce smooth results, while conservative and nearest_s2d will preserve the original coarse grid structure (although the data is now defined on a finer grid.).
nearest_d2s is quite different from others: One source point can be mapped to only one destination point. Because we have far less source points (on a low-resolution grid) than destination points (on a high-resolution grid), most destination points cannot receive any data so they just have zero values. Only the destination points that are closest to source points can receive data.
Decreasing resolution
[8]:
for method in method_list:
ds_coarse[method] = regrid(ds_in, ds_coarse, ds_in["data"], method)
[9]:
fig, axes = plt.subplots(3, 2, figsize=[8, 8])
for i, method in enumerate(method_list):
ax = axes.flatten()[i]
ds_coarse[method].plot.pcolormesh(ax=ax)
ax.set_title(method, fontsize=15)
plt.tight_layout()
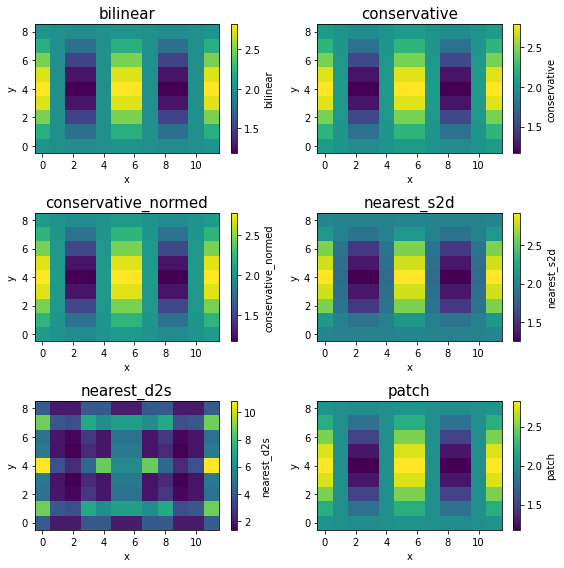
When regridding from high-resolution to low-resolution, all methods except nearest_d2s produce similar results here. But that’s largely because the input data is smooth. For real-world data, it is generally recommended to use conservative for upscaling, because it takes average over small source grid boxes, while bilinear and nearest_s2d effectively throw away most of source grid boxes.
nearest_d2s is again different: Every source point has to be mapped to a destination point. Because we have far more source points (on a high-resolution grid) than destination points (on a low-resolution grid), a single destination point will receive data from multiple source points, which can accumulate to a large value (notice the colorbar range).